Hack #1:

why is it important to know that algorithms that look different can do the same thing and that algorithms that look the same might have different results? It is important to know that algorithms look different because that way you know that there is more than one way to solve the problem and you know how to approach the code if there is something wrong with it and you can start fixing it.

for the converted conditional to boolean conversion(0.10)

am_sick = False
am_not_sick = True

# setting variables here (same as above to make comparison easier)
driveSchool = not(am_sick) and am_not_sick
if driveSchool == False:
    print("I don't want to go to school")
if driveSchool == True:
    print("I'll go to school")

I'll go to school

Hack #2:

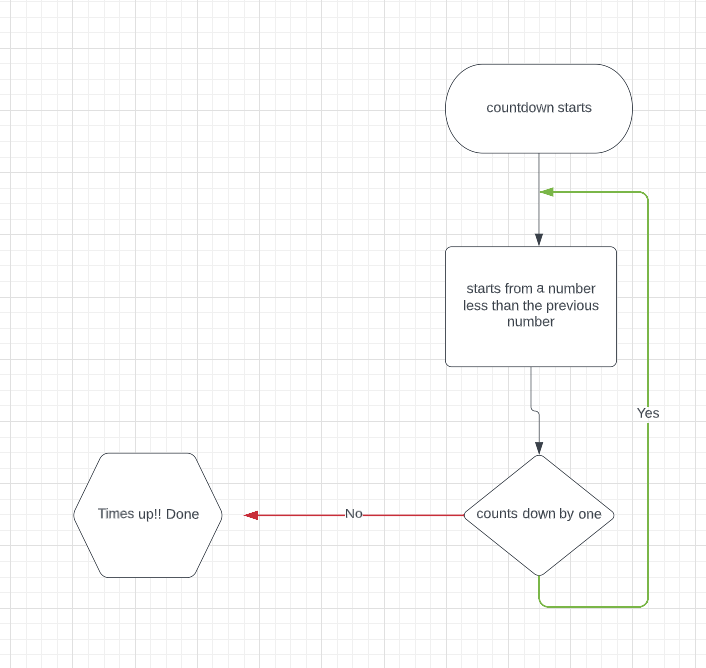
countdown = 10
while (countdown > 0):
    countdown -= 1
    print(countdown)
    if countdown == 0:
        print("Times Up!!")

9
8
7
6
5
4
3
2
1
0
Times Up!!

screenshot

Hack #3:

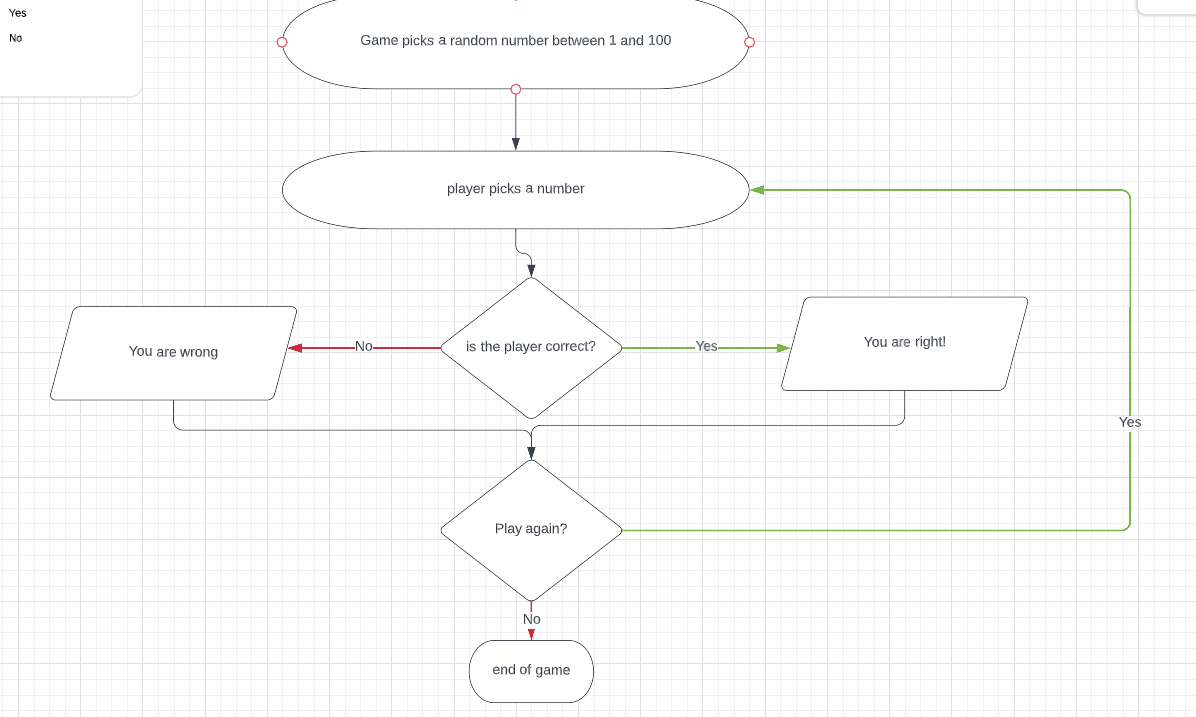
import random

#sets variables for the game
num_guesses = 0
user_guess = 0
upper_bound = 100
lower_bound = 0

#generates a random number
number = random.randint(1,100)

#print(number)     #for testing purposes

print(f"I'm thinking of a number between 1 and 100.")

#Write a function that gets a guess from the user using input()
def guess():
    #add something here
    return number #add something here 

#Change the print statements to give feedback on whether the player guessed too high or too low
def search(number, guess):
    global lower_bound, upper_bound
    if guess < number:
        print("You are bad at guessing") #change this
        lower_bound = guess
    elif guess > number:
        print("You suck :(") #change this
        upper_bound = guess
    return lower_bound, upper_bound

while user_guess != number:
    user_guess = guess()
    num_guesses += 1
    print(f"You guessed {user_guess}.")
    lower_bound, upper_bound = search(number, user_guess)
    print(f"Guess a number between {lower_bound} and {upper_bound}.")

print(f"You guessed the number in {num_guesses} guesses!")

I'm thinking of a number between 1 and 100.
You guessed 96.
Guess a number between 0 and 100.
You guessed the number in 1 guesses!

screenshot

Hacks #4:

calculate the middle index and create a binary tree for each of these lists

12, 14, 43, 57, 79, 80, 99
92, 43, 74, 66, 30, 12, 1
7, 13, 96, 111, 33, 84, 60

Binary Trees:

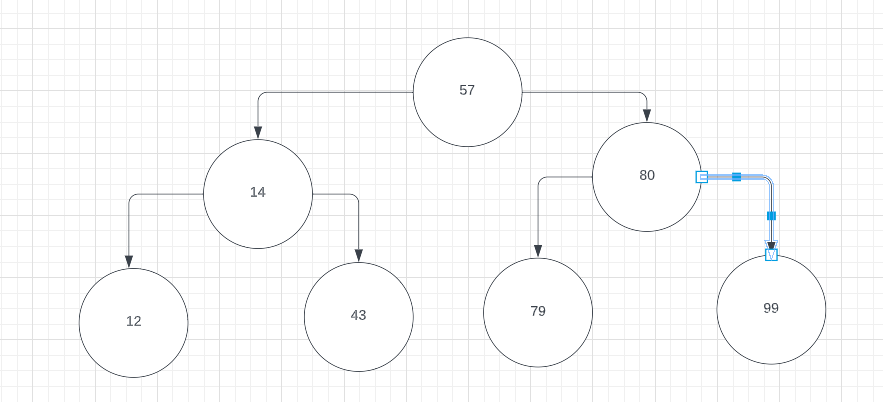
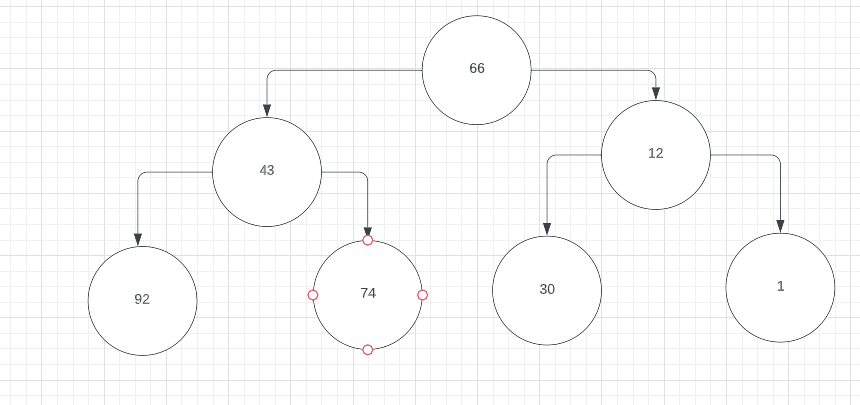
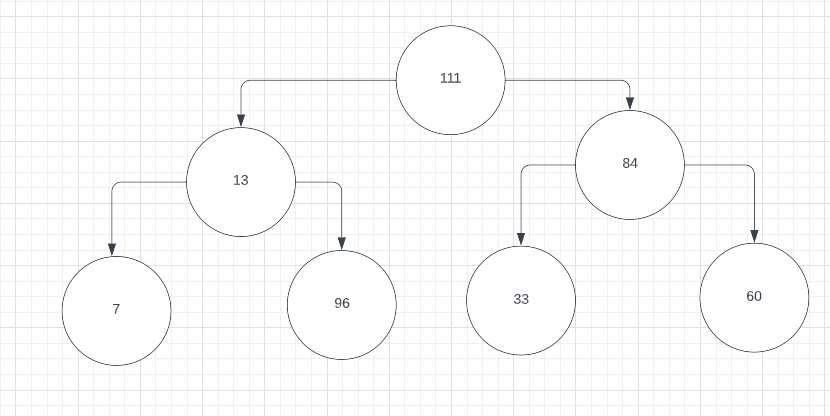
screenshot

Using one of the sets of numbers from the question above, what would be the second number looked at in a binary search if the number is more than the middle number?

For the first set, it would be 80. For the second set, it would be 12 and for the third set it would be 84.

Which of the following lists can NOT a binary search be used in order to find a targeted value?

a. ["amy", "beverly", "christian", "devin"]

b. [-1, 2, 6, 9, 19]

c. [3, 2, 8, 12, 99]

d. ["xylophone", "snowman", "snake", "doorbell", "author"]

I think that C is the correct answer because it has to go in acending order.